Abstract
I have already reported that the pyramid method is one of very effectively algolithms for summing string elements in an array using Google Apps Script (GAS). This report describes the adaptability of the pyramid method to any languages except for GAS. c++ (g++), Go, Java, Javascript on Node.js, Python and Ruby were chosen as the sample languages. In those languages, there are languages which have the distinctive commands for summing the array elements. In this report, “+” operator as a standard command and a special command for each language were used. For c++ (g++), Javascript on Node.js and Python which have no distinctive commands for summing the array elements, only “+” operator was used. For others, both “+” operator and each special command such as “[]byte”, “StringBuilder” and “<<” were used. For languages without the distinctive commands for summing, the pyramid method made us show some interesting phenomena. It was found that the pyramid method shows a good effect on only the specific language. It was found that “+” operator had been optimized for g++ and Node.js. “+” operator of Python was corresponding to theoretical results. This means that “+” operator of Python is not optimized. On the other hand, for languages with the distinctive commands for summing, it was found that the distinctive commands is incompatible to the pyramid method. These results made us show the possibility of visualization for the optimized codes.
Introduction
When the string elements in an array are summed by a script, there are various patterns for each language. A standard algorithm is the method using “+” operator as following a pseudo code.
Declare a string variable arr, sum
Declare an integer variable loopcounter
Set arr to size n
for loopcounter = 0 to (size of arr) - 1
sum = sum + arr[loopcounter]
loopcounter = loopcounter + 1
endfor
Some languages have the special commands (”[]byte”, “StringBuilder” and “<<“) for summing string elements except for “+” operator. Such languages can sum elements effectively using the special commands even if the standard method was used. However the languages which have no special commands must use only “+” operator. I had experienced that at GAS. Therefore, I have proposed the pyramid method. [1] It had been found that the pyramid method is high efficiency for summing the array elements at GAS. It is very important for today, which have increased the opportunity to handle the strings, to efficiently sum the strings. In this report, I have investigated about the adaptability of pyramid method to any languages.
Now I have 2 patterns of the standard method and the pyramid method for summing array elements. Furthermore, those 2 patterns were demonstrated by experimental and theoretical approaches. [1] I have thought that the optimization of each language may be able to be evaluated using as those tools. In this study, those tools made us show some interesting phenomena. The pyramid method showed a good effect on only the specific language using “+” operator. It was found that the languages which showed no good effect had had the optimized “+” operator. It is considered that this is due to the optimization engine of interpreters and compilers. It was found that the languages with the special commands for summing array elements are incompatible to the pyramid method. These results say that the languages with “+” operator without the optimization can benefit from the pyramid method. Also it is considered that the pyramid method can be used to evaluate the optimization engine. The result in this study gave us the possibility of visualization for optimized codes. So there are two aims of this report. One is to confirm the effects on various languages of the pyramid methods. And another is to consider the visualization of optimization engine.
For the detailed information of the standard method and the pyramid method which are used in this report, you can see them. [1]
Experimental procedure
$\Psi, \mu, \theta, \phi$ and $\omega$ which are used in this report are the total amount of active data during the summing process, the size of one array-element, the number of total array elements, the size of division for dividing array and the number of divisions for the pyramid method, respectively. The detailed information of them are here. The array used in this study is 2 dimensional array constructed with strings such as [[‘0000000’, ‘a’], [‘0000001’, ‘a’], [‘0000002’, ‘a’], ,,,]. When this array is summed, ‘,’ and ‘\n’ are added as a delimiter and an end code, respectively. So the size of an element $\mu$ becomes 10 bytes. The optimized $\omega$ and $\phi$ were obtained by report [1]. Those are $\omega=\log_{10} \theta - 1, \phi=(1/\theta)^{-1/(\omega+1)}$. The languages which were chosen for this study are shown in table 1. c++ sources were compiled by g++ (6.1.0 on msys2) with the option “-O2”. The PC spec which was used for measuring data in this study is CPU Core i5-3210M, Memory 8 GB, OS Windows10 (x64) (v1607).
Table 1: Languages used in this study.
| Language | Version |
|---|---|
| c++ | Compiler g++ (6.1.0 on msys2) |
| Go | v1.7.1 windows/amd64 |
| Java | v8 (1.8.0_101) |
| Javascript on Node.js | v6.3.0 (v8 ‘5.0.71.52’) |
| Python | v3.5.2 |
| Ruby | v2.3.1p112 |
Results and discussions
Figures 1 - 6 show the behavior of the processing time for each language with the increase in $\theta$ which is the number of array elements. All figures were put in a table. Left side shows the results taken from the measurements using “+” operator. Right side shows the results taken from the measurements using the distinctive commands of each language.
 |
|
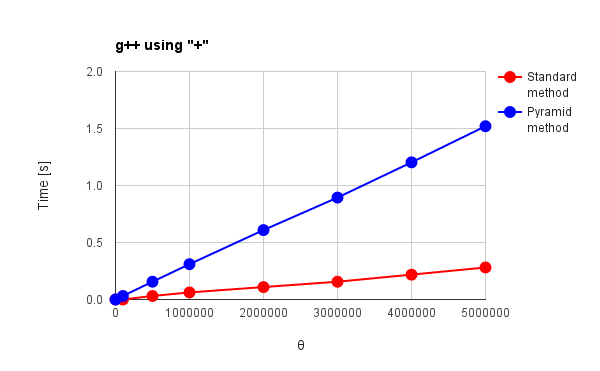
| Fig. 1: g++ using “+” | |
 |
|
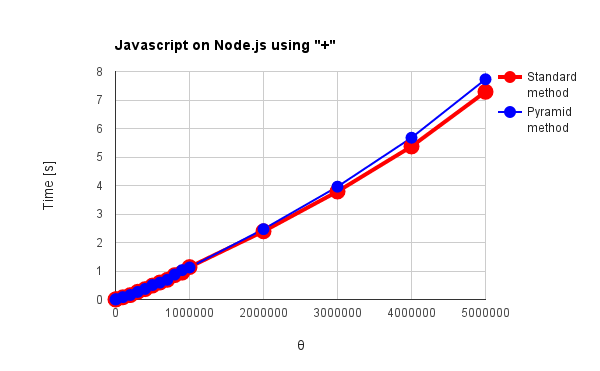
| Fig. 2: Javascript on Node.js using “+” | |
 |
|
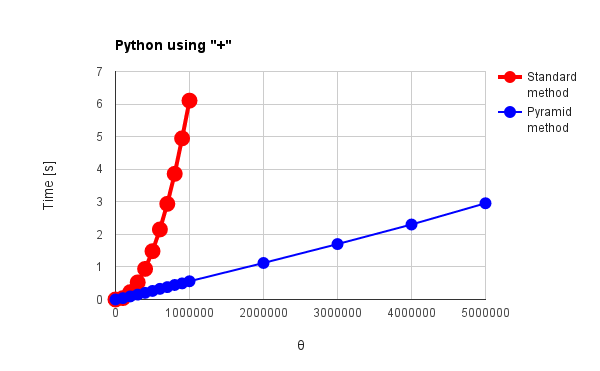
| Fig. 3: Python using “+” | |
 |
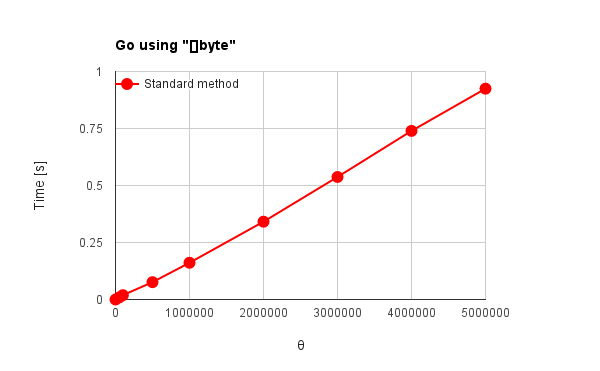 |
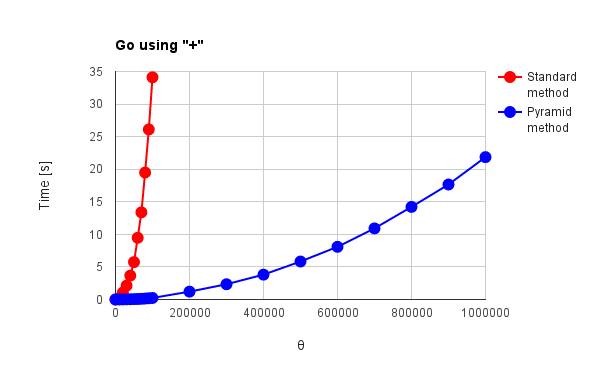
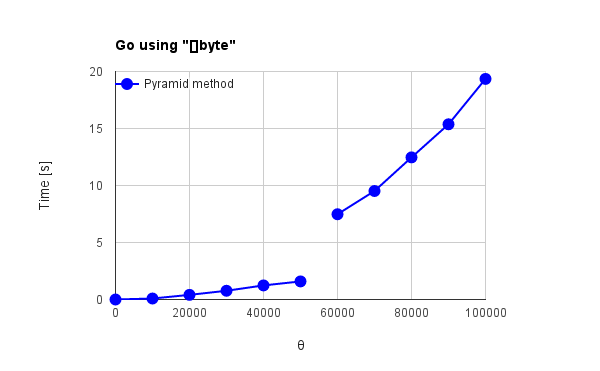
| Fig. 4(a): Go using “+” | Fig. 4(b): Go using “[]byte” |
 |
|
| Fig. 4(c): Go using “[]byte” | |
 |
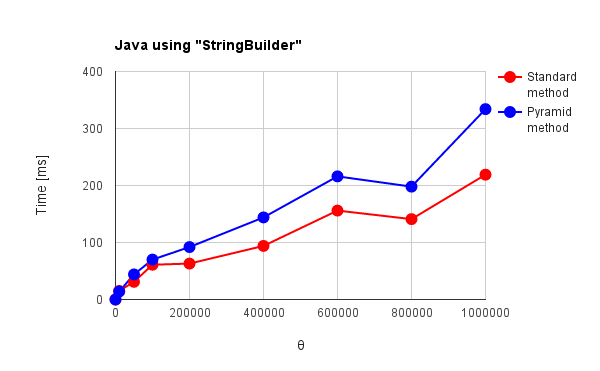 |
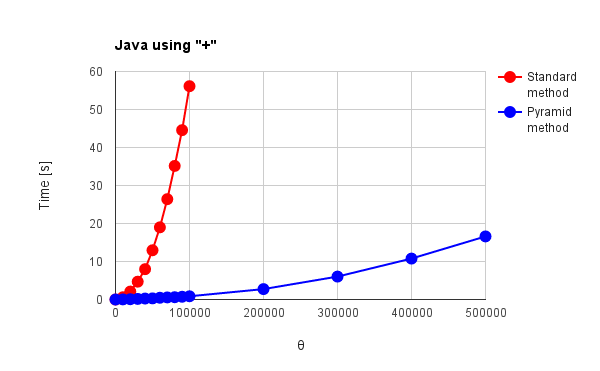
| Fig. 5(a): Java using “+” | Fig. 5(b): Java using “StringBuilder” |
 |
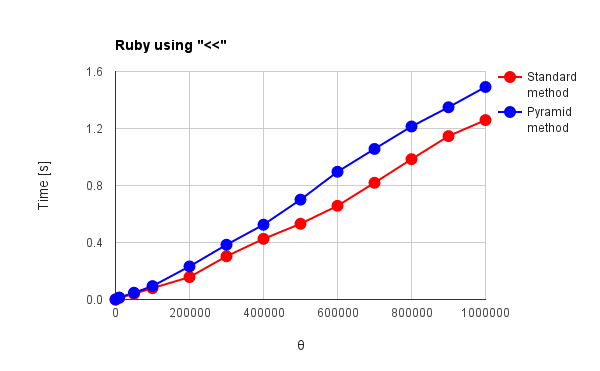 |
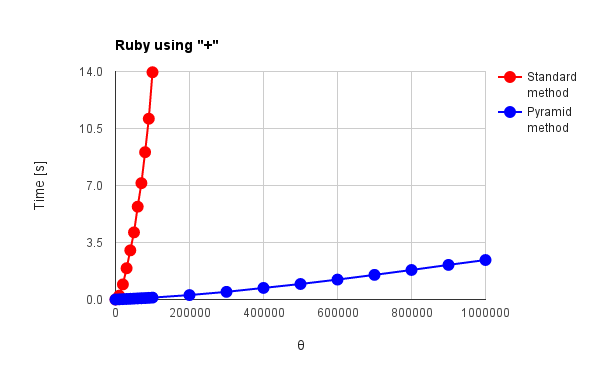
| Fig. 6(a): Ruby using “+” | Fig. 6(b): Ruby using “<<” |
g++, Node.js and Python in Figs. 1 - 3 have no distinctive commands except for “+” operator. Go, Java and Ruby in Figs. 4 - 6 have distinctive commands. For the results of “+” operator, the language except for g++ and Node.js can be confirmed the effect of the pyramid method. Especially, Python and Ruby in Figs. 3 and 6(a) show the behavior corresponding to theoretical results which had been already reported by me. [1] For the standard method, $\Psi$, which is the total amount of active data during summing, increases proportionally to the square of $\theta$. For the pyramid method, $\Psi$ linearly increases with the increase in $\theta$. Go and Java in Figs. 4(a) and 5(a) show the increase of $\Psi$ proportionally to the square of $\theta$ for both red and blue lines. The optimization may influence to the process of pyramid method. g++ and Node.js in Figs. 1 and 2 show no effect of the pyramid method. It is considered that “+” operator is optimized for g++ and Node.js which have no special commands for summing array elements. V8 engine of Node.js is known as one of the optimization engines. The optimization may influence to only the standard method or disturb the work of pyramid method. For Go, Java and Ruby which have the special commands for summing, the pyramid method shows no effect as shown in Figs. 4(b), 4(c), 5(b) and 6(b). Also it is considered that this is due to the optimization. In Figs. 1, 2, 4(b), 5(b) and 6(b), $\Psi$ linearly increases with the increase in $\theta$ for the standard method. Furthermore, the reverse phenomenon that the process speed of standard method becomes faster than that of pyramid method occurs in those figures. These clearly show the optimization of summing process. In order to consider these, it thinks of the number of loops during summing process. The number of loops $N_{l}$ during summing process can be expressed as follows.
\[ N_{l} = \sum_{k=1}^{\omega - 1} \frac{\theta}{\phi^{k}} \tag{1} \]
From Eq. (1), $N_{l0} = \theta$ at $\omega=0$ and $N_{li} = \theta(1 - \phi^{-1})^{-1}$ at $\omega=\infty$ can be obtained. Therefore, the increasing rate $\varepsilon$ from $N_{l0}$ to $N_{li}$ becomes as follows.
\[ \varepsilon = 100 \times \frac{1}{(\phi - 1)} \tag{2} \]
where the unit is $\%$. $\omega = 0$ and $\omega \geqq 1$ mean the standard and the pyramid method, respectively. Here, since this study was performed under the condition of $\theta = 1,000,000$ and $\phi = 10$, $\varepsilon$ is $11\%$ and the number of loops of the pyramid method increases 11,000 for that of the standard method under this condition. In this study, the number of loops for the pyramid method is $11\%$ larger than that of the standard method. Then, I think that when the languages for summing process are optimized, the search of last address of each string is much faster than that of languages without the optimization. By these, when the languages have the special commands for summing array elements and the optimized “+” operator, it is considered that the processing time strongly depends on the number of loops in the code rather than $\Psi$. Therefore, it is considered that the reverse phenomenon occurs for the processing time between the standard and the pyramid method as shown in Figs. 1, 2, 5(b) and 6(b). And the reverse phenomenon is remarkable, since the speed of g++ is much faster than that of other languages.
Here, when Figs. 2 and 6(b) are compared, it is found that both behaviors of $\Psi$ for the increase in $\theta$ are almost the same. At $\theta = 1,000,000$ of the standard method, the processing time is 1.13 s and 1.25 s for Node.js and Ruby, respectively. It may indicate that both optimization is almost the same.
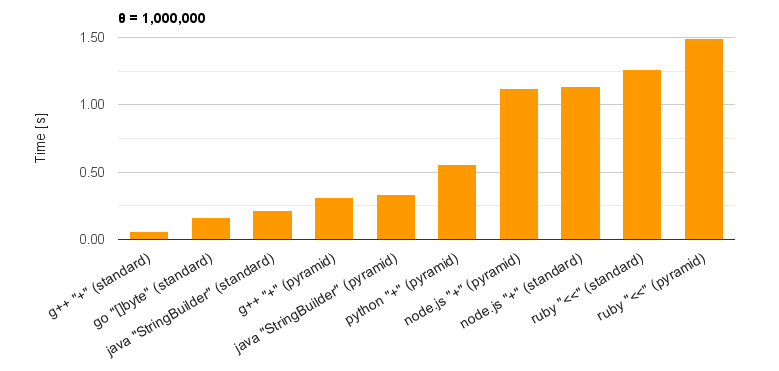 |
| Fig. 7: Top 10 data of processing time for each language at $\theta = 1,000,000$. |
Figure 7 shows the summing process-time for each language at $\theta = 1,000,000$. The top 10 data are shown in Fig. 7. This figure shows the high performance of languages (g++, Go and Java) compiled by the compiler. There is two interesting points. 1st point is the result of Python using the pyramid method. Python using the pyramid method shows 2 times faster in the processing speed than Node.js with V8 engine. When it thinks that the processing time of Python using the standard method at $\theta = 1,000,000$ is 6.1 s, this is the remarkable data for the pyramid method. And for $\theta = 5,000,000$, the processing speed of Python is 2.6 times faster than that of Node.js. In the 2nd point, for Go and Ruby, it was found that “[]byte” and “<<” are predominantly optimized compared to “+” operator.
From the results in this study, it was found that the pyramid method is efficient for languages except for GAS. Especially, languages corresponding to the trend of theoretical results are more efficiently. Languages, which have distinctive optimized commands for summing array elements, should use both the special commands and the standard method. Languages which needs to compile should use the standard method. These results can also be used to the visualization of optimization engine.
Summary
Following results could be obtained in this study.
The pyramid method for summing array elements is efficient for the languages except for GAS.
Languages with “+” operator without the optimization can benefit from the pyramid method.
Languages, which have distinctive optimized commands for summing array elements, should use both the special commands and the standard method.
The pyramid method can be used to evaluate the optimization engine.
The result in this study gave us the possibility of visualization for optimized codes.
Reference
[1] “Improved Algorithms for Summation of Array Elements”, October 13, 2016
Appendix
Scripts used at this report are here.