Abstract
I considered an efficient algorithm for summation of array elements. All elements in an array are string. When those elements are summed using scripts, a standard method is to add each element in order. If the script is run without any optimize, the process becomes gradually sluggish, because the total amount of active data during the summation process is proportional to the square of the number of array elements. This leads directly to the high process-cost. Such phenomenon notably appears at Google Apps Script (GAS). This report says about the solution of this problem using a new algorithm of a pyramid method. The pyramid method achieves that the total amount of active data increases proportional to the linear of the number of array elements. By this, the processing time becomes much shorter than that of the process using the standard method. The pyramid method achieved the process-cost reduction of $99.7%$ compared with the standard method at GAS. I realized again that new discoveries are hidden into the familiar scenes of every-day life.
Introduction
What script comes to mind when you hear the summation of string elements in an array? Most people will probably imagine the method for adding each element in order as following a pseudo code.
Declare a string variable arr, sum
Declare an integer variable loopcounter
Set arr to size n
for loopcounter = 0 to (size of arr) - 1
sum = sum + arr[loopcounter]
loopcounter = loopcounter + 1
endfor
It can be said that these are a standard algorithm. When the number of elements is small, this standard method is so useful for the summation. But when the number is large, the summation process becomes sluggish. The reason is that the total amount of active data increases proportionally to the square of the number of array elements. Namely, it means that summing array elements in order leads to high process-cost. High process-cost connects directly to large money and time loss. The summation process is used at variety situations. Recently, the array with string elements are used at the field of big data and, web technology and so on. Therefore, it is very important to design the effective summation algorithms with lower process-cost.
In this report, an efficient algorithm for summing string elements in an array is introduced. The key factor for this algorithm is to change the total amount of active data during the summation process. At the standard method, the summation process of array elements makes the total amount of active data increase proportionally to the square of number of array elements. On the other hand, at the algorithm in this report, the total amount of active data linearly increases to the number of array elements. This difference is very important for reducing the process cost.
The primary aim of this report is to reduce the process cost during the summation process. The secondary aim is to reduce the burden for Google when we run the summation process of array elements using Google Apps Script (GAS). GAS is one of good resources which can be used by only browser. It is important to reduce the process cost of GAS by devising. Therefore, the samples which were used in this report were made of GAS. At next section, theoretical approaches will be introduced.
Theoretical approaches
Array element which is used in this report is string. In order to understand the pyramid method which is introduced in this report, it thinks about the total amount of active data during the summation process. When the array elements are summed by the standard method as shown in Introduce section, the total amount of active data $\Psi$ during the process is
\[ \Psi = \sum_{\lambda=1}^{\theta} \mu \lambda \tag{1} \]
where $\mu$ and $\theta$ are the size of one array-element and the number of array elements, respectively.
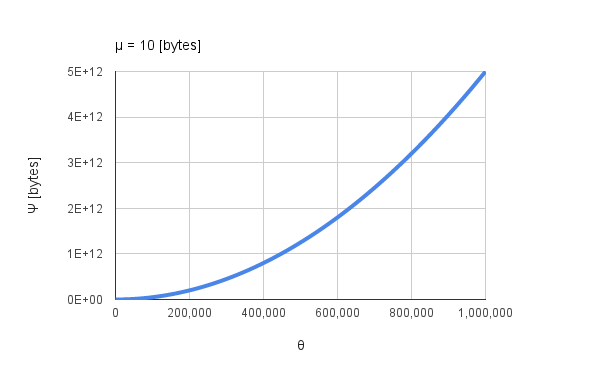 |
| Fig. 1: $\Psi$ vs. $\theta$ by Eq.(1). |
Figure 1 shows $\Psi$ vs. $\theta$ when $\mu$ is 10 bytes. It is found that $\Psi$ increases proportionally to the square of $\theta$ as shown in Fig.1. I have thought that the processing time has to correlate to the total amount of active data $\Psi$ during the process. In order to reduce $\Psi$, I propose a pyramid method. The pyramid method calculates the sum while dividing $\theta$ to some groups as shown in Fig. 2.
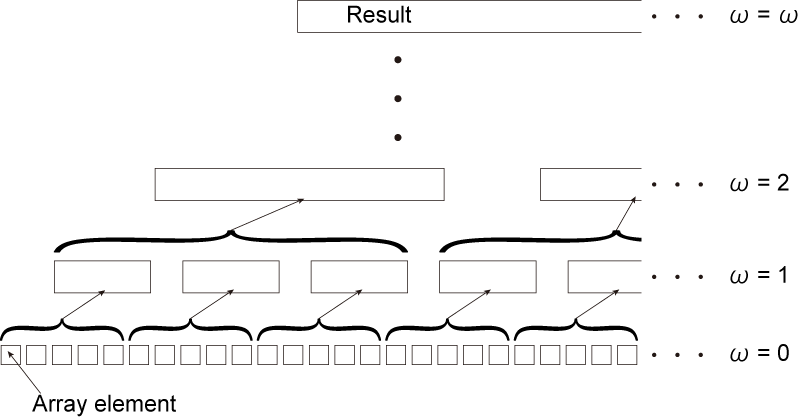 |
| Fig. 2: Concept of pyramid method. |
At the pyramid method, the base array without dividing is $\omega=0$ in Fig. 2. At $\omega=1$, $\theta$ is divided to groups by $\phi$ determined as a division number. The array elements in each group is summed. This flow is performed until obtaining the result. As a sample, it shows a pseudo code with the pyramid method at $\omega=1$ obtained from Fig. 2.
Declare a string variable arr, tempsum, sum
Declare an integer variable division, loopcounter1, loopcounter2
Set arr to size n
division = d
for loopcounter1 = division to (size of arr) - 1
for loopcounter2 = 0 to (size of arr) - 1
tempsum = tempsum + arr[loopcounter2]
loopcounter2 = loopcounter2 + 1
endfor
sum = sum + tempsum
tempsum = ''
loopcounter2 = loopcounter1
loopcounter1 = loopcounter1 + division
endfor
When this code is compared to the code at Introduction, it notices that a loop for grouping is added. The array is divided at first loop. The array elements in each group is summed at second loop. When $\omega$ increases, the loops for grouping is increased.
Here, it considers $\Psi(\omega)$ for Fig. 2. $\Psi(\omega)$ can be expressed as following an equation.
$ \theta_{\omega} $
\[ \Psi(\omega) = \left(\sum_{\lambda=1}^{\phi_1} \mu_{1} \lambda\right)\frac{\theta_{1}}{\phi_{1}} + \left(\sum_{\lambda=1}^{\phi_2} \mu_{2} \lambda\right)\frac{\theta_{2}}{\phi_{2}} + \cdots \]
\[ + \left(\sum_{\lambda=1}^{\phi_{\omega-1}} \mu_{\omega-1} \lambda\right)\frac{\theta_{\omega-1}}{\phi_{\omega-1}}\]
\[ + \left\{\left(\sum_{\lambda=1}^{\phi_{\omega}} \mu_{\omega} \lambda\right)\frac{\theta_{\omega}}{\phi_{\omega}} + \sum_{\lambda=1}^{\frac{\theta_{\omega}}{\phi_{\omega}}} \mu_{\omega}\phi_{\omega}\lambda \right\} \tag{2} \]
where $\phi$ is a division number. $\theta_{\omega}$ and $\mu_{\omega}$ are $ \theta\phi^{1-\omega} $ and $ \mu\phi^{\omega-1} $, respectively. Equation (2) can be expanded as follows.
\[ \Psi(\phi, \omega) = \frac{\mu\theta}{2}\left\{ \left(\phi + 3\right)\omega + \frac{\theta}{\phi^{\omega}} - 1 \right\} \tag{3} \]
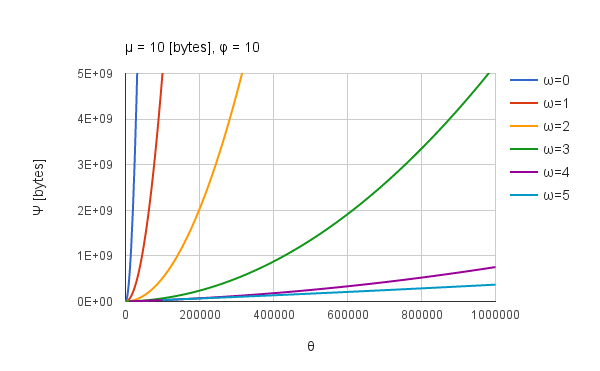 |
| Fig. 3: $\Psi$($\phi$, $\omega$) vs. $\theta$. $\mu$ and $\phi$ are constant. $\omega$ is changed from 0 to 5. |
Figure 3 shows $\Psi(\phi, \omega)$ vs. $\theta$. $\mu$ and $\phi$ are constant. $\omega$ is changed from 0 to 5. A line of $\omega=0$ is same to Fig. 1. From Fig. 3, it is found that $\Psi(\phi, \omega)$ for $\theta$ strongly depends on $\omega$. Also it is found that the change of $\Psi(\phi, \omega)$ approaches the linear increase to $\theta$ with the increase in $\omega$. Then, $\Psi(\phi, \omega)$ becomes small with the increase in $\omega$. It must pay attention that the available $\theta$ changes with the increase in $\omega$. Under $\phi = 10$, when $\omega$ is 2, $\theta$ must be more than 1000. For $\omega=5$, $\theta$ must be more than 1,000,000. The optimized $\phi$ can be obtained by the partial derivative of $\Psi(\phi, \omega)$ with respect to $\phi$ as shown in Eq.(4).
\[\frac{d\Psi(\phi, \omega)}{d\phi} = \frac{\mu\theta\omega}{2}\left( 1 - \theta \phi^{-(\omega+1)} \right) \tag{4} \]
When $d\Psi(\phi, \omega)/d\phi$ is 0,
\[ \phi = \left( \frac{1}{\theta} \right)^{-\frac{1}{\omega+1}} \tag{5} \]
For example, when $\theta$ and $\omega$ are 1,000,000, 5, respectively, $\phi=10$ is obtained using Eq. (5). The optimized $\omega$ can be obtained by deforming Eq.5 as follows.
\[ \omega = \log_{\phi} \theta-1 \tag{6} \]
In order to obtain optimized $\omega$ and $\phi$, either $\omega$ or $\phi$ has to be known. Therefore, at first, it is necessary to decide either $\omega$ or $\phi$. So, $\phi=10$ is used in this study.
I have already talked that the processing time have to correlate to the total amount of active data $\Psi$ during the process. From theoretical results, the ratio of $\Psi$ for the standard and the pyramid method is 13,514 at $\theta = 1,000,000$. If my estimation is correct, it is considered that the ratio of processing time for the standard and the pyramid method will be large.
The results of theoretical approaches indicate that the pyramid method is useful for the summation of array elements. At next section, experimental data will show the predominance of pyramid method against the standard method using GAS.
Experimental results
The sample array used in this study is 2 dimensional array like [[‘0000000’, ‘a’], [‘0000001’, ‘a’], [‘0000002’, ‘a’], ,,,]. When this array is summed, ‘,’ and ‘\n’ are added as a delimiter and end code, respectively. The size of an array element $\mu$ is 10 bytes. All array-elements are string.
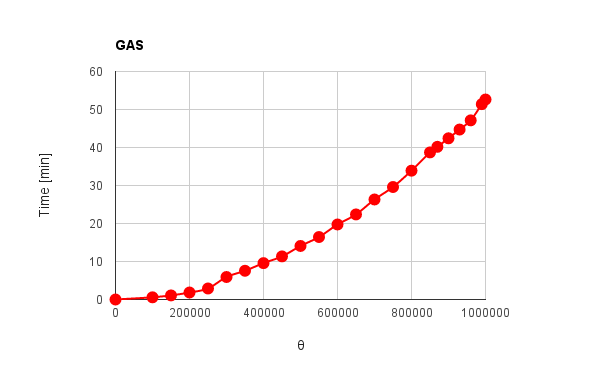 |
| Fig. 4: Processing time vs. $\theta$ using GAS with standard method. |
Figure 4 shows the processing time vs. $\theta$ obtained using the standard method by GAS. This data was obtained using a trigger command of GAS. The actual script can be seen at last section. It was found that the processing time of about 52 minutes are necessary for summing 1,000,000 array elements. Also it was found that the processing time increases proportionally to the square of $\theta$. Also this can be confirmed by the fitting function. This trend in Fig.4 is almost the same to that in Fig. 1. Namely, when the summation process is run, the change of $\Psi$ and the processing time have a correlation. In order to clarify the effect of pyramid method, the processing time vs. $\theta$ using GAS with pyramid method was measured.
 |
| Fig. 5: Processing time vs. $\theta$ using GAS with pyramid method. |
Figure 5 shows the processing time vs. $\theta$ using GAS with the pyramid method. For the pyramid method, under $\phi=10$, $\omega$ was optimized by the results obtained at the section of Theoretical approaches. Namely, $\omega$ and $\phi$ are changed in accordance with the number of digits of $\theta$. Each data-point was measured 10 times and adopted the average value with error bar. From Fig. 5, it was found that the processing time of the summation process becomes drastically short by adopting the pyramid method. The array elements of 1,000,000 could be summed in about 8 seconds. This is the process-cost reduction of $99.7%$ compared with Fig. 4. Also it was found that the pyramid method changes the slope of the processing time with the increase in $\theta$ to the linear proportion. This trend corresponds to the prediction at Theoretical approaches. This is indicated that the reduction of the amount of active data during the summation process leads to reducing the process cost. From Figs. 4 and 5, it can be said that the pyramid method is very useful for the summation process with string elements in an array. Furthermore, the pyramid method is easy to apply to the filed of parallel computing. It is considered that the pyramid method can be applied to the parallel computing by giving the summation process of each group to each thread. By this, the efficiency will be much higher.
Summary
I reported about the pyramid method for summing the string elements in an array and obtained following results.
-
The pyramid method could reduce the process cost of GAS for summing the string elements in an array. In the case of 2 dimensional array used in this study, the pyramid method succeed in the process-cost reduction of $99.7%$ compared with the standard method. Is this also Pyramid Power? ;)
-
It was found that the pyramid method is an effectively algorithm for summing the string elements in an array.
-
It was found that the amount of active data during processing strongly depends on the processing time.
-
It is considered that if the code during running is optimized in any process, the amount of active data during processing dependence on the processing time will be weak. (You can see the report which confirmed this at here.)
Acknowledgements
I would like to thank Google and Google staff.
Appendix
Library for GAS
A library for GAS using the pyramid method is here.
Scripts used at this report
Scripts used at this report are here.