Kanshi Tanaike
Introduction
Please be careful! This result can be only used for Google Apps Script.
There are a limit executing time for Google Apps Script (GAS). That is 6 minutes.1 So users always have to pay attention to reducing the process cost of the scripts. Especially, it is very important to know the process cost for the array processing, because the array processing is often used for spreadsheet and Google APIs. I have already reported “Benchmark: Loop for Array Processing using Google Apps Script”.2 At February 7, 2020, the V8 runtime got to be able to be used in my account. By this, it is considered that it is possibly changed the result of benchmark without V8 2. So I measured about this. In this report, the process cost of “loop” for the array processing using GAS has been investigated with V8 runtime.
When users use the loop process for the array using GAS, the following 6 methods can be considered.
- Normal “for loop”
for (var i = 0; i < 10; i++) {array[i]}
- for in
for (var i in array) {array[i]}
- while
while (i < 10) {array[i++]}
- forEach
array.forEach(function(e){e})
- map, filter
array.map(function(e){e})array.filter(function(e){e})
- reduce
array.reduce(function(ar,e){e},[])
- for of
for (var e of array) {e}
- for of with iterator
for (var e of array[Symbol.iterator]()) {e}
As the result, it was found that when v8 runtime is used, the process costs of methods except for “for in” were almost the same for the array processing of both 1 dimensional and 2 dimensional array. The process costs of “for loop”, “while”, “forEach”, “map, filter” and “reduce” were not changed with increasing the array length. At “for in”, when the array length is large, the process cost was linearly increased. Also it was found that at GAS, the cost of push() and new Array() was almost the same.
Note: When v8 runtime is used, the comprehension like
[e for each (e in array)]cannot be used. In this case, when the script is saved, an error occurs. Please be careful this.
About the difference with and without V8 runtime, it was found that when v8 runtime is used for the loop process, the process cost could be largely reduced. For all methods of “for loop”, “for in”, “while”, “forEach”, “map, filter” and “reduce”, the process costs of 15709 % for 1D array and 253887 % for 2D array in the average were reduced. About “for of” and “for of with iterator”, these cannot be used without V8. So in this case, the values of 15709 % and 253887 % don’t include them.
Experimental procedure
As the samples of array, 1 dimensional and 2 dimensional array were used. The array processing was performed by “for loop”, “for in”, “while”, “forEach”, “map, filter” and “reduce”. The process time was measured and the results were compared. Then, when we see the scripts for the array processing at various sites, push() is often used. As another way, there is the way for using new Array(). In this report, the process costs of push() and new Array() were also compared. In order to measure the process cost of array processing, the script which retrieves the multiple of 5 from the elements of arrays was used as a sample script. The sample scripts of Google Apps Scripts which were used for this report are here. a For measuring the process cost, the cost for creating array to use at the methods is not included. By the way, at GAS, the processing time is not stable as you know. So the average value for more than 100 times measurements was used for each data point which is shown by figures. At this time, the fluctuation of the average values was less than 1 %. I worry that each detailed-data point at my environment might be different from that at other user’s environment. But I think that the trend of this result can be used.
In this report, in order to compare the process costs with and without V8 runtime, exactly the same scripts used at Benchmark: Loop for Array Processing using Google Apps Script was used.
Results
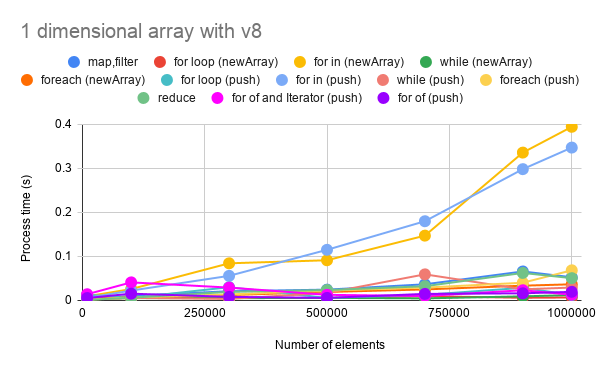
Fig 1. Number of elements vs. processing time for 1 dimensional array.
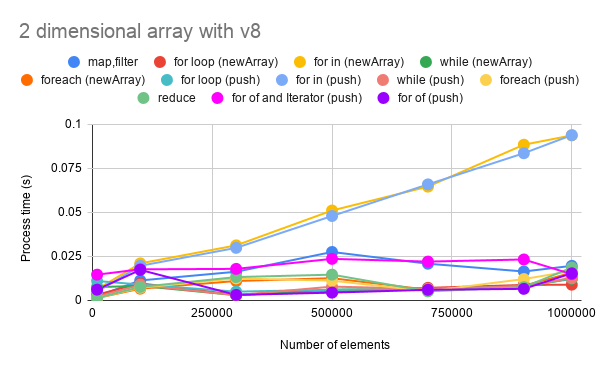
Fig 2. Number of elements vs. processing time for 2 dimensional array.
Figures 1 and 2 show that the number of elements vs. processing time for 1 and 2 dimensional arrays, respectively. The results of push() and new Array() are also included in these figures.
From both figures, it can be seen the 2 patterns. One is the lines which linearly increase. Another is the lines in almost parallel to the X-axis. The lines which linearly increases are “for in”. The lines in almost parallel to the X-axis are “for loop”, “while”, “forEach”, “map, filter”, “reduce” , “for of” and “for of with iterator”. From these lines in almost parallel to the X-axis, it is found that the process costs of “for loop”, “while”, “forEach”, “map, filter”, “reduce”, “for of” and “for of with iterator"are almost the same.
Here, when “for of” and “for of with iterator” are compared, the cost of “for of” is a bit lower than that of “for of with iterator”. It is considered that this is due to the cost for creating the iterator.
Also it is found that at GAS, the costs of push() and new Array() were almost the same. This is the interesting result. This is the important result for using Google Apps Script with V8 runtime.
Here, it can be seen that the process cost of 1D array is higher than that of 2D array. At the 1D array, when the number of element is increased, the number of element in the 1D array is increased. On the other hand, at the 2D array, even when the number of element is increased, each array length of 2D array is 1,000. It means that the 1D array, which is the element of 2D array, is the constant length. Then, when the number of element is increased, the number of each element in 2D array is increased. It is considered that it is due to this different. For example, it supposes that the process costs for 1D and 2D arrays are measured with the condition of the number of element of 1,000,000. In this case, at 1D array, 1,000,000 elements are put in an array and it is measured. At 2D array, 1,000,000 elements are that one 1D array of 1,000 elements is put in an array of 1,000 times.
Compare process costs with and without V8
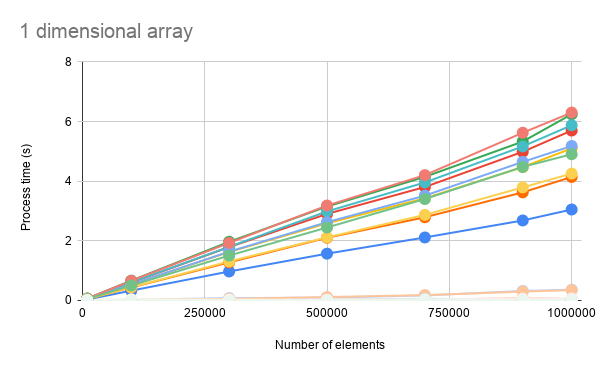
Fig 3. Process costs with and without V8 for 1 dimensional array.
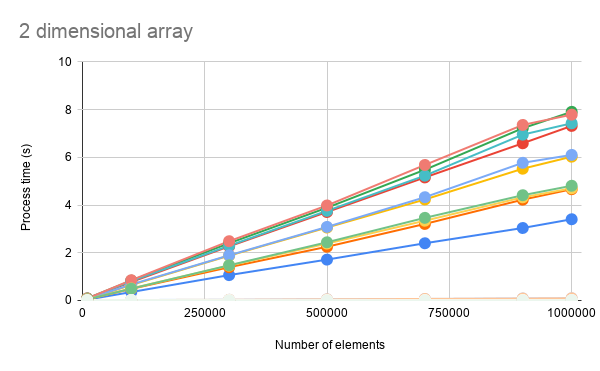
Fig 4. Process costs with and without V8 for 2 dimensional array.
As the additional discussion, here, the comparison of the process costs with and without V8 is introduced. The results without V8 can be seen at here.
About the difference with and without V8 runtime, it was found that when v8 runtime is used for the loop process, the process cost could be largely reduced. For all methods of “for loop”, “for in”, “while”, “forEach”, “map, filter” and “reduce”, the process costs of 15709 % for 1D array and 253887 % for 2D array in the average were reduced. In this case, when all result values with and without V8 are put in a chart, the lines of the values with V8 are the same with the X-axis as shown in Figs. 3 and 4. From this result, it is considered that to use V8 runtime can largely improve the performance of the loop process ofGoogle Apps Script.
Table 1: Reduction (percentage) of the process cost When V8 is enabled under the same script. The calculation method is (Result_with_V8 - Result_without_V8) / Result_with_V8.
| Methods | 1D | 2D |
|---|---|---|
| map,filter | -4464% | -202033% |
| for loop (newArray) | -40788% | -241181% |
| for in (newArray) | -1601% | -50574% |
| while (newArray) | -41573% | -200235% |
| foreach (newArray) | -8886% | -258614% |
| for loop (push) | -23059% | -171697% |
| for in (push) | -1782% | -54261% |
| while (push) | -19505% | -256434% |
| foreach (push) | -7431% | -253924% |
| reduce | -7999% | -253887% |
| for of | - | - |
| for of with iterator | - | - |
| Average | -15709% | -253887% |
About “for of” and “for of with iterator”, these cannot be used without V8. So in this case, the values of 15709 % and 253887 % don’t include them.
Summary
In this report, the process cost of “loop” for the array processing using GAS with using V8 runtime has been investigated. As the result, it was found the following important features for GAS with V8.
- In the case of the sample script for retrieving the multiple of 5 from the array, the loop costs using “for loop”, “while”, “forEach”, “map, filter”, “reduce”, “for of” and “for of with iterator” are almost the same.
- In the case of “for in”, the process cost is higher than those of “for loop”, “while”, “forEach”, “map, filter”, “reduce”, “for of” and “for of with iterator”. But when that is compared with the condition without V8, the cost of “for in” with V8 is much lower than those without V8.
- Costs of
push()andnew Array()are almost the same. - When v8 runtime is used for the loop process, the process cost could be largely reduced when it is compared with the script without V8.
- For all methods of “for loop”, “for in”, “while”, “forEach”, “map, filter” and “reduce”, the process costs of 15709 % for 1D array and 253887 % for 2D array in the average were reduced.
As a note, I have to describe that this is the result for Google Apps Script. For other languages, this result might be difference. And also, the process cost of this report might be modified by future update of Google.
References
- Current limitations at Quotas for Google Services
- Benchmark: Loop for Array Processing using Google Apps Script without V8
Appendix
Scripts
The scripts, which were used with this report, are the same with Benchmark: Loop for Array Processing using Google Apps Script without V8. (Except for the comprehension script.)
Creating sample arrays
The function for creating 1 dimensional array is as follows.
function make1dArray(row) {
var ar = [];
for (var i = 0; i < row; i++) {
ar[i] = i + 1;
}
return ar;
}
The function for creating 2 dimensional array is as follows.
function make2dArray(row) {
var ar1 = [];
for (var i = 0; i < row; i++) {
var ar2 = [];
for (var j = 0; j < 100; j++) {
ar2[j] = j + 1;
}
ar1[i] = ar2;
}
return ar1;
}
For 1 dimensional array
// for loop using push()
var result = [];
for (var i = 0; i < array.length; i++) {
if (array[i] % 5 == 0) {
result.push(array[i]);
}
}
// for loop using new Array()
var result = new Array(array.length / 5);
var c = 0;
for (var i = 0; i < array.length; i++) {
if (array[i] % 5 == 0) {
result[c++] = array[i];
}
}
// for in using push()
var result = [];
for (var i in array) {
if (array[i] % 5 == 0) {
result.push(array[i]);
}
}
// for in using new Array()
var result = new Array(array.length / 5);
var c = 0;
for (var i in array) {
if (array[i] % 5 == 0) {
result[c++] = array[i];
}
}
// while using push()
var result = [];
var i = 0;
while (i < array.length) {
if (array[i] % 5 == 0) {
result.push(array[i]);
}
i += 1;
}
// while using new Array()
var result = new Array(array.length / 5);
var c = 0;
var i = 0;
while (i < array.length) {
if (array[i] % 5 == 0) {
result[c++] = array[i];
}
i += 1;
}
// forEach using push()
var result = [];
array.forEach(function(e) {
if (e % 5 == 0) {
result.push(e);
}
});
// forEach using new Array()
var result = new Array(array.length / 5);
var c = 0;
array.forEach(function(e) {
if (e % 5 == 0) {
result[c++] = e;
}
});
// map, filter
var result = array.filter(function(e) {
return e % 5 == 0;
});
// reduce
var result = array.reduce(function(o, e) {
if (e % 5 == 0) o.push(e);
return o;
}, []);
// for of
var result = [];
for (var e of array) {
if (e % 5 == 0) {
result.push(e);
}
}
// for of with iterator
var it = array[Symbol.iterator]();
var result = [];
for (var e of it) {
if (e % 5 == 0) {
result.push(e);
}
}
For 2 dimensional array
// for loop using push()
var result = [];
for (var i = 0; i < array.length; i++) {
var temp = [];
for (var j = 0; j < array[i].length; j++) {
if (array[i][j] % 5 == 0) {
temp.push(array[i][j]);
}
}
result.push(temp);
}
// for loop using new Array()
var result = new Array(array.length);
for (var i = 0; i < array.length; i++) {
var temp = new Array(100 / 5);
var c = 0;
for (var j = 0; j < array[i].length; j++) {
if (array[i][j] % 5 == 0) {
temp[c++] = array[i][j];
}
}
result[i] = temp;
}
// for in using push()
var result = [];
for (var i in array) {
var temp = [];
for (var j in array[i]) {
if (array[i][j] % 5 == 0) {
temp.push(array[i][j]);
}
}
result.push(temp);
}
// for in using new Array()
var result = new Array(array.length);
var c1 = 0;
for (var i in array) {
var temp = new Array(100 / 5);
var c2 = 0;
for (var j in array[i]) {
if (array[i][j] % 5 == 0) {
temp[c2++] = array[i][j];
}
}
result[c1++] = temp;
}
// while using push()
var result = [];
var i = 0;
while (i < array.length) {
var temp = [];
var j = 0;
while (j < array[i].length) {
if (array[i][j] % 5 == 0) {
temp.push(array[i][j]);
}
j += 1;
}
result.push(temp);
i += 1;
}
// while using new Array()
var result = new Array(array.length);
var i = 0;
while (i < array.length) {
var temp = new Array(100 / 5);
var c = 0;
var j = 0;
while (j < array[i].length) {
if (array[i][j] % 5 == 0) {
temp[c++] = array[i][j];
}
j += 1;
}
result[i] = temp;
i += 1;
}
// forEach using push()
var result = [];
array.forEach(function(e) {
var temp = [];
e.forEach(function(f) {
if (f % 5 == 0) {
temp.push(f);
}
});
result.push(temp);
});
// forEach using new Array()
var result = new Array(array.length);
array.forEach(function(e, i) {
var temp = new Array(100 / 5);
var c = 0;
e.forEach(function(f) {
if (f % 5 == 0) {
temp[c++] = f;
}
});
result[i] = temp;
});
// map, filter
var result = array.map(function(e) {
return e.filter(function(f) {
return f % 5 == 0;
});
});
// reduce
var result = array.reduce(function(o, e) {
var temp = e.reduce(function(p, f) {
if (f % 5 == 0) p.push(f);
return p;
}, []);
o.push(temp);
return o;
}, []);
// for of
var result = [];
for (var e of array) {
var temp = [];
for (var f of e) {
if (f % 5 == 0) {
temp.push(f);
}
}
result.push(temp);
}
// for of with iterator
var it1 = array[Symbol.iterator]();
var result = [];
for (var e of it1) {
var it2 = e[Symbol.iterator]();
var temp = [];
for (var f of it2) {
if (f % 5 == 0) {
temp.push(f);
}
}
result.push(temp);
}